Introduction
Finding the median of two arrays ? This isn't just about finding the median of two arrays. Its about finding the median efficiently.
Disclaimer : This problem is one of the problems that really hurt my soul (and brain). It's a pretty long read, so brace yourself. The algorithm at the end is so beautiful that understanding it comes with a price of immense demotivation and questioning your existence as a developer (if you are one).
The problem
This is a problem from leetcode, Median of Two Sorted Arrays.
The problem states that you have been given two arrays of lengths m and n respectively, which are sorted in non-decreasing order and your job is to find out the median of the merged sorted array. (sounds easy right ?)
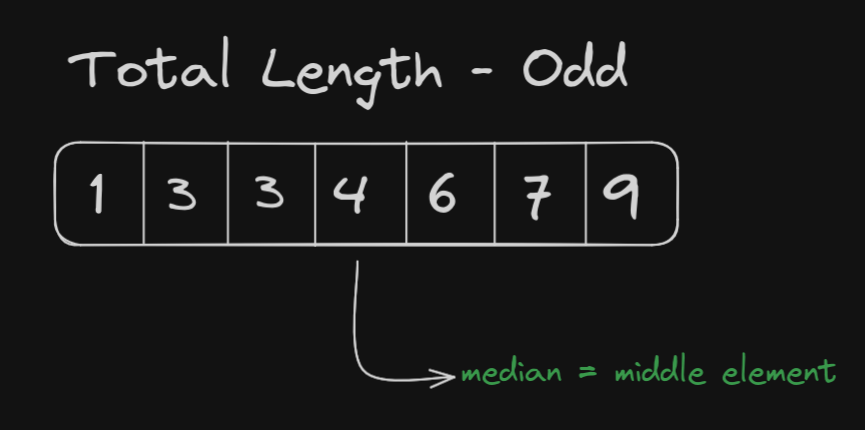
Pre-requsite - What is a median ?
Before going into the solution, it's crucial to understand what exactly we mean by the "median" of an array. In a array of integers (not necessarily sorted), the median is the middle element if the array length is odd. If the array length is even, it's the average of the two middle elements.

Approach
Initial Thought Process - The Bruteforce
The most straight-forward approach is to follow what the question states - merge both arrays, sort them, and find the median. This method would work even if the arrays are not sorted initially.
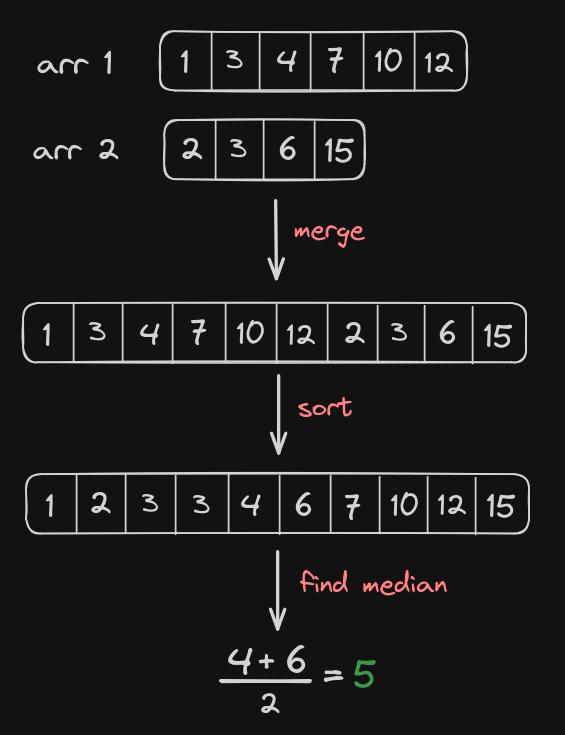
The time complexity is O((m+n)log(m+n)) due to concatenation and sorting.
The space complexity is O(m+n) for the merged array.
I thought of doing a one liner in python just to see if it worked
class Solution:
def findMedianSortedArrays(self, a: List[int], b: List[int]) -> float:
import statistics
return statistics.median(a+b)
The results were as follows
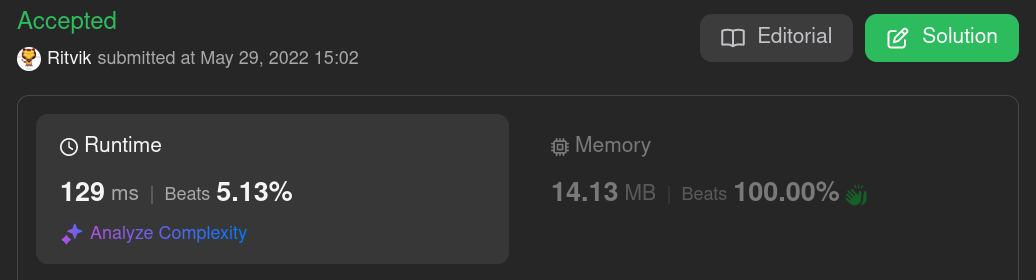
The runtime sucks , memory usage is good.
Then I felt really bad for doing DSA using inbuilt libraries, that too in python (sorry python guys). Then I wrote the same code in cpp, knowing that nothing would change.
class Solution {
public:
double findMedianSortedArrays(vector<int>& a, vector<int>& b) {
for (int x : b) a.push_back(x);
sort(a.begin(), a.end());
int n = a.size();
if (n & 1) return a[n / 2];
else return (a[n / 2 - 1] + a[n / 2]) / 2.0;
}
};
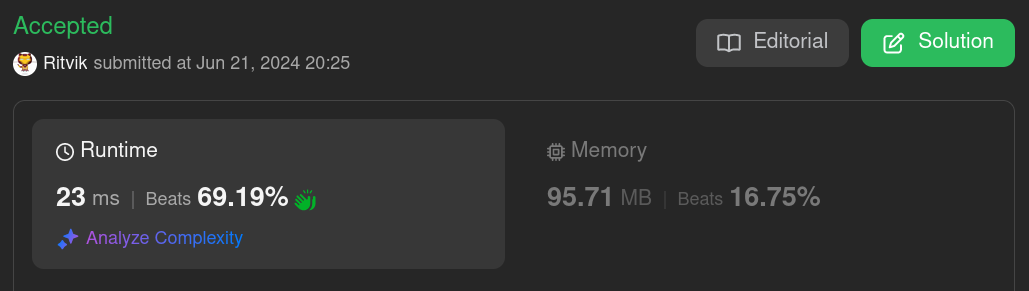
The results were as follows; major improvement in runtime, memory usage sucks.
A Better Solution - MergeSort Technique
As both the given arrays are sorted, we can exploit this sorted nature and apply the merge technique used in mergesort algorithm to reduce the complexity (time).
This method is pretty easy, create an array with a size equal to (m+n), traverse through the given arrays simulataenously, add the minimum element to the created array.
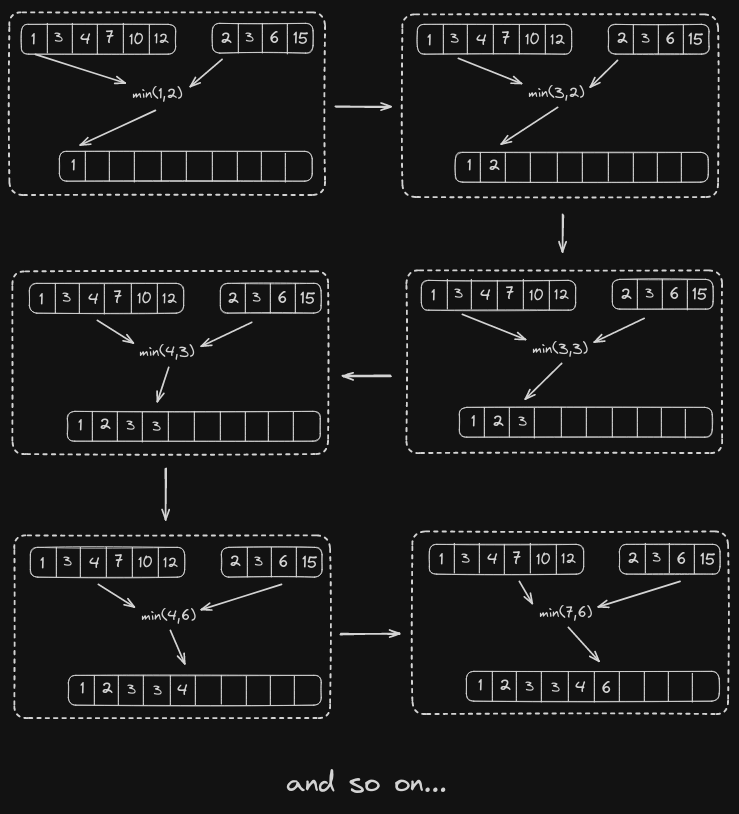
After forming the merged (and sorted) array, we determine the median.
The code is as follows
class Solution {
public:
double findMedianSortedArrays(vector<int>& a, vector<int>& b) {
int n1 = a.size();
int n2 = b.size();
int n = n1 + n2;
vector<int> merged(n);
int i = 0, j = 0, k = 0;
while (i < n1 && j < n2) {
if (a[i] < b[j]) {
merged[k++] = a[i++];
} else {
merged[k++] = b[j++];
}
}
while (i < n1) {
merged[k++] = a[i++];
}
while (j < n2) {
merged[k++] = b[j++];
}
if (n & 1) {
return merged[n / 2];
} else {
return (merged[n / 2 - 1] + merged[n / 2]) / 2.0;
}
}
};
This worked, but still the time and space usages were not that good.
The time complexity is O(m+n) due to the merge.
The space complexity is O(m+n) for the merged array.
A More-Better Solution - Two Pointer Approach
The mergesort approach was good enough. But, why use an extra array to store all the numbers when we only want a single number (the median) ?
So, I just used a two-pointer approach to keep track of the indices of the sorted array without using a sorted array (you'll get it once you look at the code).
class Solution {
public:
double findMedianSortedArrays(vector<int>& a, vector<int>& b) {
int m = a.size();
int n = b.size();
int total = m + n;
int i = 0, j = 0;
int prev = 0, curr = 0;
for (int count = 0; count <= total / 2; count++) {
prev = curr;
if (i < m && (j >= n || a[i] <= b[j])) curr = a[i++];
else curr = b[j++];
}
if (total % 2 == 1) return curr;
else return (prev + curr) / 2.0;
}
};
YESS ! A significant improvement in time and space.
The time complexity is O(m+n) due to the merge.
The space complexity is O(1). (Finally)
One final look at the question
Oh hell nah.
Logarithmic runtime ? This is where the insanity begins.
We have only got a linear time complexity till now. How the heck can this be done in logarithmic ?
Now if you are a active problem solver, you would know that logarithmic time complexity can be achieved by only a handful of algorithms such as Range queries (in segment trees and fenwick trees), union find with path compression using inverse Ackermann function (in graphs), binary exponentiation (for integers), balanced BST finds (binary search tree) and most importantly, for the arrays given in the question - BINARY SEARCH.
How the heck binary search ?
If you are thinking we will sort the merged arrays using quicksort and apply a Binary Search, its not the case as the complexity would become O((m+n)log(m+n)) due to the nature of sorting algorithms. We want a logarithmic runtime with unity coefficient, ie. O(log(m+n)). (insanity intensifies)
If we are to apply Binary Search directly on the given arrays, an important question may arise. The two given arrays are sorted independently, how can we apply a single binary search on a disjoint set ?
Are we going to apply two-pass binary search, one for each array ? But we need to know the elements of both the disjoint arrays to find the answer.
Who told anything about applying Binary Search on the arrays given in the question. We are going to apply the Binary Search on answer that most suits the question.
These types of algorithms are a subset of the Binary Search algorithms known as Binary Search on Answer (BSA) algorithms.
Understanding BSA algorithms
Firstly, the primary objective of the Binary Search algorithm is to efficiently determine the appropriate half to eliminate, thereby reducing the search space by half. It does this by determining a specific condition that ensures that the target is not present in that half.
In a normal Binary Search, we apply the algorithm on the question to find the answer. But in BSA, we know the possible range of answers and apply Binary Search on the range to find the optimum answer that perfectly suits the question.
These algorithms can be a bit tricky to explain and understand at first, but is easier to understand with a simple example.
Consider an algorithm to find the square root (as integer) of a number.
To find sqrt(n), one method is to go through all possible numbers from 1 to n to see if its square matches to n.
This is just performing a linear search on the range 1 to n to find a number that squares to n, ie. performing linear search on a range of numbers. When this Linear Search is converted to Binary Search, the algorithm becomes a BSA algorithm.
int sqrt(int n) {
int low = 1, high = n, mid;
while (low <= high) {
mid = (low + high) / 2;
int val = mid * mid;
if(val==n) return mid;
else if (val < n) low = mid + 1;
else high = mid - 1;
}
return high;
}
Although this code snippet has potential integer overflow bugs, it can be considered a basic example for BSA algorithm.
The Optimal Algorithm - Using BSA
This is the algorithm that would make a developer question his/her existence for not thinking about this approach.
For the sake of simplicity, let the given two arrays in the question be a and b of lengths n1 and n2 respectively, and let n=n1+n2.
We would first build up the initution on a case when n is even, from there we would get idea of the case of n is odd.
Now what do we apply binary search on ?
As we are applying Binary Search on Answer algorithm, let us look at the final sorted array that gives the answer first to find a possible range.

Now we can see that the sorted array contains all the elements of both the given arrays (obviously)
Let us look at them seperately and see which elements contribute to the medians.
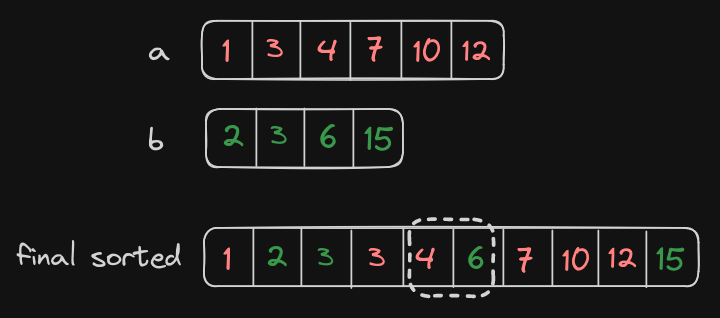
As the median is only contributed by elements in the extreme ends of the midpoint, we can partition the final sorted array into two equal subarrays, left half and right half, each of length n/2.
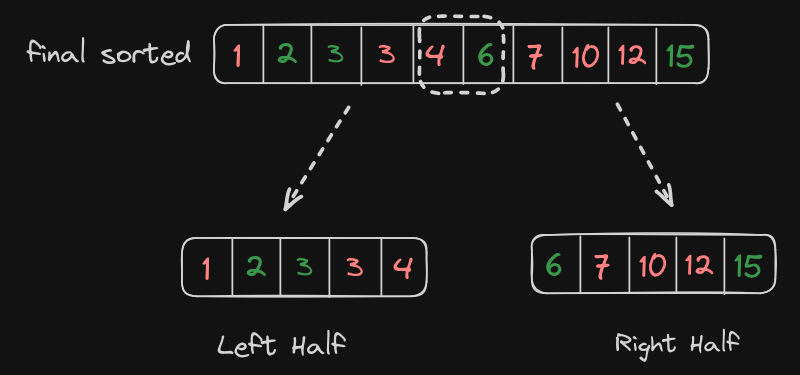
Now when we seperate the elements of each array from left and right halfs, we can see something interesting.
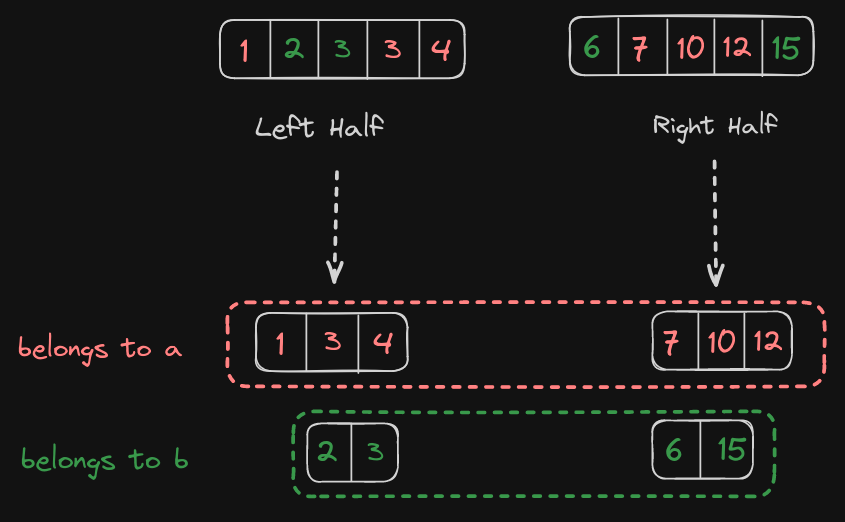
Now we can make an two interesting observations.
If you have observed and concluded that the median of the final sorted array is at the midpoint of both the individual arrays, you are exactly wrong and it is only for this case.
The first observation is that the seperated elements occur in the same order as they were in their initial arrays.

The Second observation to be made is that if one half consists of x elements from a, it consists of n/2-x elements from b. Similarly, if other half consists of y elements from a, it consists of n/2-y elements from b.
Now we are to find two variables x and y. But this can be reduced down to a single variable x by establishing a relationship between x and y using the array sizes. We know that x+y=n1, so we can replace y by x-n1.
I know it's starting to hurt your brain, but it can be understood with the help of this diagram.
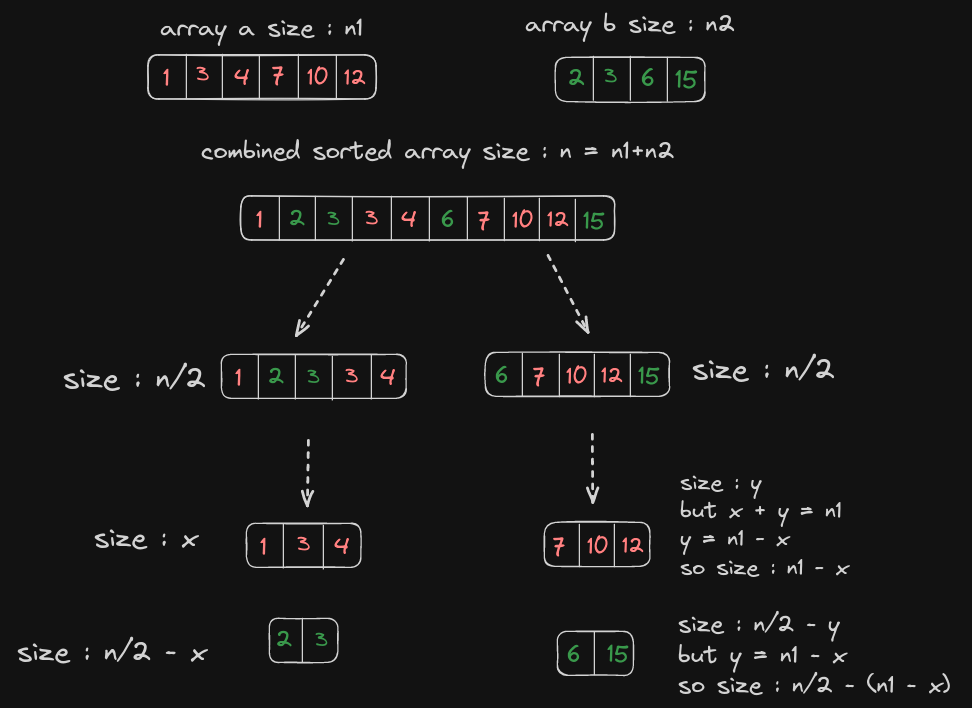
So if we find the variable x, we can partition both the arrays such that each half consists of the desired elements in order.
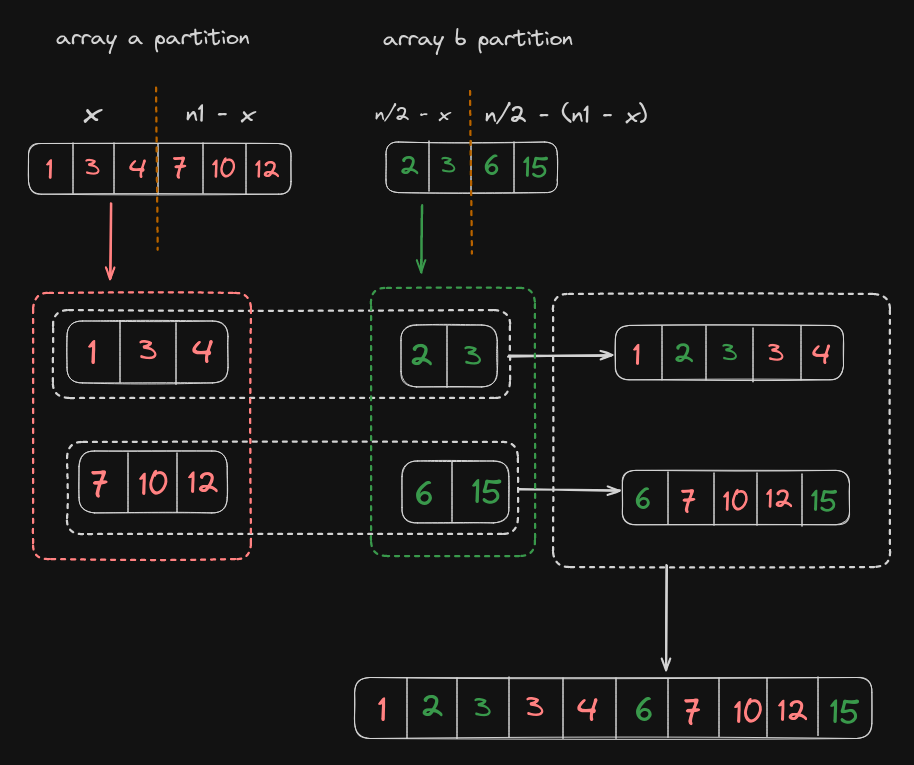
The variable x is nothing but the number of elements from array a in the left half.
Now, how do we find x using BSA algorithm ?
If we were to partition an array for length x, the minimum length of the partition would be zero (not one as the partition can be empty) and the maximum length of the partition can be the total size of array (n1 or n2).
Now we can either partition array a or array b to find x; but our goal here is to optimize the algorithm.
Consider the case where array a has a size of 1024 and array b has a size of 33554432. If we were to find x on array b using Binary Search, we would require log(33554432)=25 operations. But if we were to find x on array a, we would require only log(1024)=10 operations.
So we partition the array of smallest length to find x.
Now, on what criteria do we eliminate the search space using binary search?
We have now established the search space for x to be the range from 1 to min(n1,n2). But for a binary search to operate, we need elimination criteria to eliminate either half during the search operation.
To determine the criteria, we go through certain cases of the algorithm with respect to x established so far considering array a to be the smallest array.
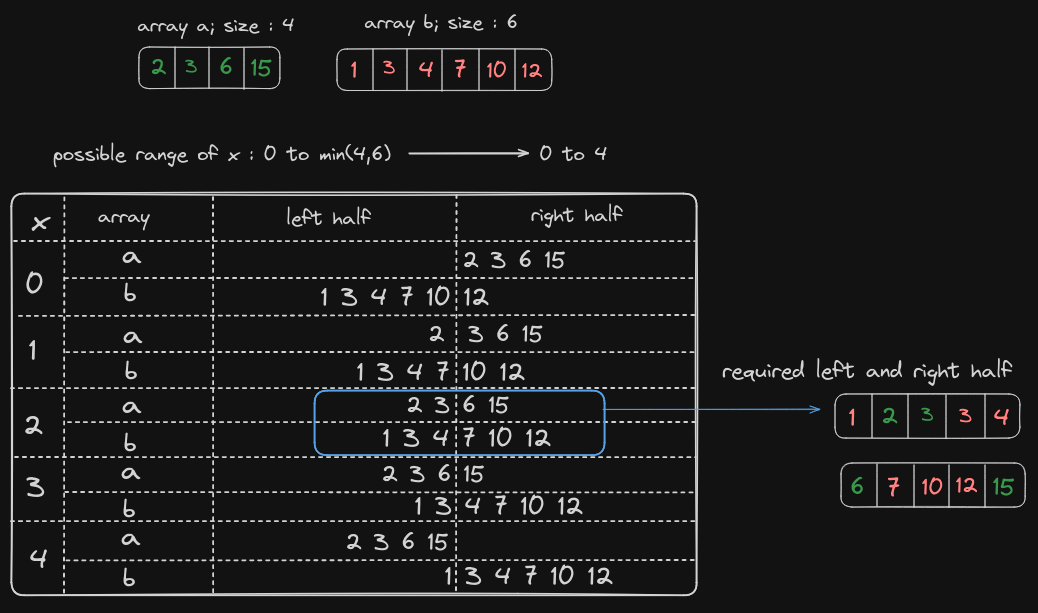
This might look a bit intimidating at first, but once you understand it and try tracing the algorithm yourself, it'll be clear.
Now, it can be seen that the optimum value of x in this case is 2. Now to find the elimination criteria, we make an observation.
After the partition, let us consider the nearest left element to the partition in array a is L1, and nearest right element to the partition in array a is R1.
Similarly, let us consider the nearest left element to the partition in array b is L2, and nearest right element to the partition in array b is R2.
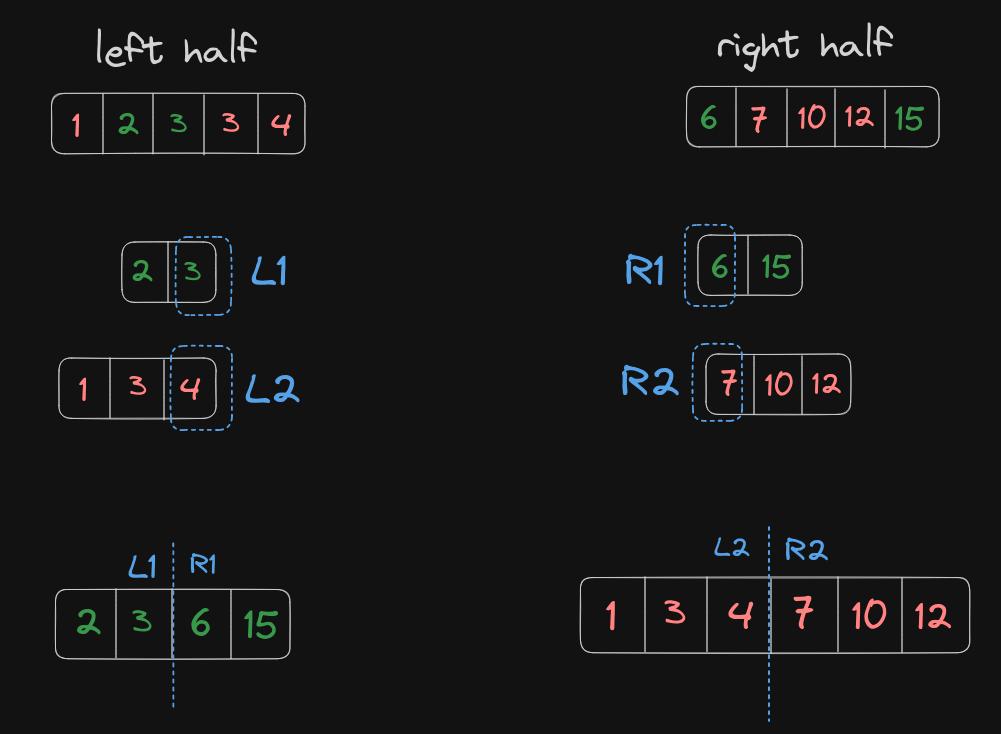
Looking at the partition, we can figure out an efficient elimination criteria.

If you look closely, whenever L2 > R1, we need to increment x, ie. eliminate the left half; and whenever L1 > R2 we need to decrement x, ie. eliminate the right half. The optimum condition is reached when L1 < R2 and L2 < R1, stopping the binary search algorithm (frickin mind blowing).
Now x is found. How to get the median ?
By observation, we can see that on reaching the optimum condition, when n is even, the median is simply given by (max(l1,l2)+min(r1,r2))/2.
If n is odd, the both halfs may not be equal, one may have one element extra. So the median is simply the extra element in the larger half.
Putting it all together
From the knowlege we have gained, we can now code the most optimum solution.
But there's a catch. We have told that we will find x only on the array with minimum length. Say, we are finding x on array a thinking its minimum length. But what if its not ? Then swapping array a and b will take O(n) complexity again ? Back to square one ? No! There is a simple way to bypass it by returning the function recursively with the parameters swapped (frickin cool again).
For those who didn't get it, look at the code snippet to understand.
double findMedian(vector<int> &a, vector<int> &b){
int n1 = a.size(), n2=b.size();
if(n1>n2) return findMedian(b,a);
/*
Rest of the code
*/
}
So instead of swapping the whole vectors that takes a complexity of O(n), we intelligently just changed the parameter order and returned it so that it is done in O(1) complexity (1000 IQ move).
The optimal Code
Finally after all these work, we are now left with a optimized O(log n) code.
class Solution {
public:
double findMedianSortedArrays(vector<int>& a, vector<int>& b) {
int n1 = a.size(), n2 = b.size();
if (n1 > n2) return findMedianSortedArrays(b, a);
int n = n1 + n2;
int t = (n1 + n2 + 1) / 2;
int low = 0, high = n1;
while (low <= high) {
int x = (low + high) >> 1;
int y = t - x;
int l1 = INT_MIN, l2 = INT_MIN;
int r1 = INT_MAX, r2 = INT_MAX;
if (x < n1) r1 = a[x];
if (y < n2) r2 = b[y];
if (x - 1 >= 0) l1 = a[x - 1];
if (y - 1 >= 0) l2 = b[y - 1];
if (l1 <= r2 && l2 <= r1) {
if (n % 2 == 1) return max(l1, l2);
else return ((double)(max(l1, l2) + min(r1, r2))) / 2.0;
} else if (l1 > r2) high = x - 1;
else low = x + 1;
}
return -1;
}
};
The results were satisfying.
This is code with the required time complexity.
The time complexity is O(log(m+n)) due to BSA algorithm. (As requested)
The space complexity is O(1). (Perfect)
Going beyond Optimal Code
Although the code was of the most optimum time and space complexity, I felt it still wasnt fast enough as the BSA was not the fastest compared to the two pointer approach. We only managed to reduce the complexity of the algorithm. Why not use a few performance boosting tricks to make the code even faster.
So I switched off the synchronization of c++ input-output streams with that of the C io-stream.
So I just added these two lines of code in the first line of the function
std::ios_base::sync_with_stdio(false);
std::cin.tie(nullptr);
class Solution {
public:
double findMedianSortedArrays(vector<int>& a, vector<int>& b) {
std::ios_base::sync_with_stdio(false);
std::cin.tie(nullptr);
int n1 = a.size(), n2 = b.size();
if (n1 > n2) return findMedianSortedArrays(b, a);
int n = n1 + n2;
int t = (n1 + n2 + 1) / 2;
int low = 0, high = n1;
while (low <= high) {
int x = (low + high) >> 1;
int y = t - x;
int l1 = INT_MIN, l2 = INT_MIN;
int r1 = INT_MAX, r2 = INT_MAX;
if (x < n1) r1 = a[x];
if (y < n2) r2 = b[y];
if (x - 1 >= 0) l1 = a[x - 1];
if (y - 1 >= 0) l2 = b[y - 1];
if (l1 <= r2 && l2 <= r1) {
if (n % 2 == 1) return max(l1, l2);
else return ((double)(max(l1, l2) + min(r1, r2))) / 2.0;
} else if (l1 > r2) high = x - 1;
else low = x + 1;
}
return -1;
}
};
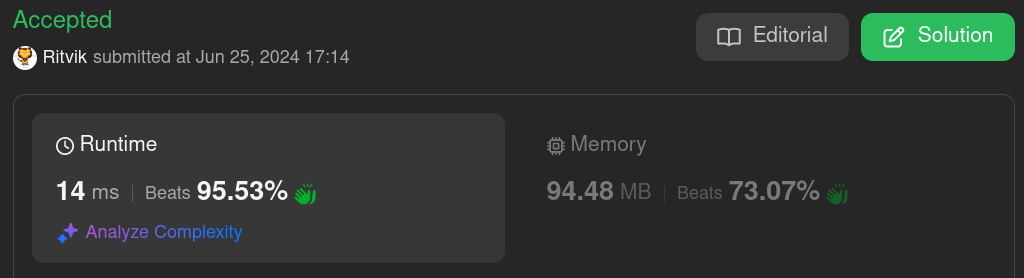
YESSS. Now we have reached a point where the code is the most optimum.
Or is it ?
A minor Issue
If you look closely, for a trained eye, you can see that the de-synchronization of c++'s standard io-stream can happen twice if the recursive function is called. This can cause a minor performance issue. To solve it, I placed the de-synchronization code below the recursive call such that it is called only once even if the code runs recursively.
The Perfect Code
Now after all the optimizations done, I have changed the previous code a little bit. The algorithm is the same but just the structuring is different.
The main motive here now is speed, and this is the most optimized code as far. It's okay if you're not able to understand it.
class Solution {
public:
double findMedianSortedArrays(vector<int>& a, vector<int>& b) {
int n1 = a.size(), n2 = b.size();
if (n1 > n2) return findMedianSortedArrays(b, a);
std::cin.tie(NULL);
std::ios_base::sync_with_stdio(false);
int n = n1 + n2;
int t = (n + 1) / 2;
int low = 0, high = n1;
while (low <= high) {
int x = (low + high) >> 1;
int y = t - x;
int l1 = (x > 0) ? a[x - 1] : INT_MIN;
int l2 = (y > 0) ? b[y - 1] : INT_MIN;
int r1 = (x < n1) ? a[x] : INT_MAX;
int r2 = (y < n2) ? b[y] : INT_MAX;
if (l1 <= r2 && l2 <= r1) return (n&1) ? max(l1, l2) : (max(l1, l2) + min(r1, r2)) / 2.0;
else if (l1 > r2) high = x - 1;
else low = x + 1;
}
return -1;
}
};
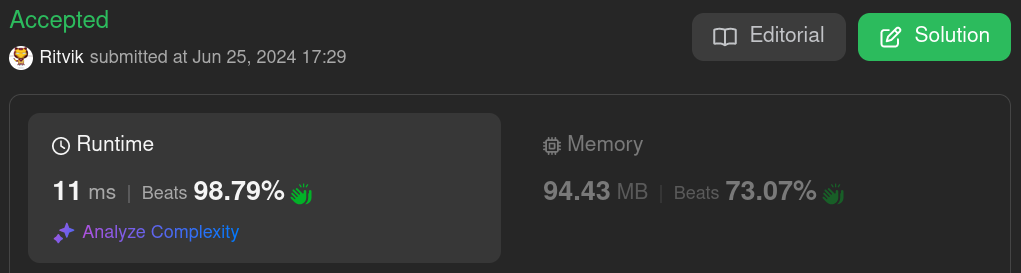
Now I can sleep peacefully :)
This code beats the runtime by 98.79% and beats the space by 73.07% making it the most optimal code that can solve this problem.
We have brought down the runtime from 129ms to 11ms, which is a pretty big thing for a hard problem.
Now, if you have come so far, but didn't understand much, it's okay as this is a pretty complex problem.
If you have understood everything till now, congratulations, you have successfully understood the inituition and solution of one of the depressing problems on leetcode.
If you found the most optimal solution in the beginning itself, using BSA just by seeing the question for the first time, congratulations, you are not a human being.