Introduction
In the realm of coding and algorithm design, optimization isn't just a luxury; it's a necessity. The difference between a brute force approach and an optimized one can be the difference between a solution that runs for hours and one that completes in milliseconds. It can mean the difference between a user waiting endlessly and a seamless user experience. Especially in real-world applications, where efficiency is paramount, mastering the art of optimization becomes critical. Here's how I tackled one such problem, evolving my solution step by step, from an elementary brute force method to an efficient and elegant one.
The problem
This is a problem from leetcode, Searching a 2D matrix II.
The problem states to write an efficient algorithm that searches for a value target in an m x n integer matrix which has the following properties:
- Integers in each row are sorted in ascending from left to right.
- Integers in each column are sorted in ascending from top to bottom.
The Bruteforce
My first instinct was not to solve the problem efficiently, but to solve the problem.
So I did a trivial apporach, what a lay man would do - ran a nested loop, iterating over every single element to find the target.
This was the code -
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size();
int n = matrix[0].size();
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(matrix[i][j]==target) return true;
}
}
return false;
}
};
If you're a competetive programmer, I know, you would be yelling at me right now.
The time complexity sucks - O(n²), considering the constraints given (maximum matrix size 300x300), yes it was dead slow.
Here are the results:
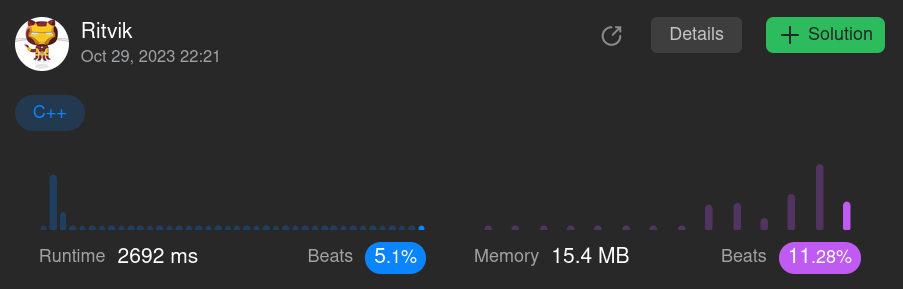An astounishing 2.7 second runtime :)
I was not expecting it to pass the checks. It should have been a timeLimtExceeded error, but maybe it was a mere luck.
The failure
Who gets the right solution when optimizing the first time ?
I thought of a divide and conqurer approach and went for it, trying to exploit the sorted nature of the matrix.
Here is the code
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size();
int n = matrix[0].size();
int rlo=0,rhi=m-1,clo=0,chi=n-1;
while(rlo<=rhi && clo<=chi){
int rmid = rlo+(rhi-rlo)/2;
int cmid = clo+(chi-clo)/2;
if(matrix[rmid][cmid]==target) return true;
else if(matrix[rmid][cmid]>target){
if(target-matrix[rmid-1][cmid]<target-matrix[rmid][cmid-1]) rhi = rmid-1;
else chi = cmid - 1;
} else {
if(matrix[rmid+1][cmid]-target > matrix[rmid][cmid+1]-target) clo = cmid+1;
else rhi = rmid - 1;
}
}
return false;
}
};
Although this looks like it would work, it dosen't. I wanted to share this because this approach has a fatal flaw. This approach completely ignores a qudrant of a matrix each time, which is not supposed to be done as the rows and columns are sorted independently.
First Optimization
After a few minutes of thinking, I found the approach. I thought why not of starting from right corner, if the target is smaller than the current element, I move left, if larger, I move down.
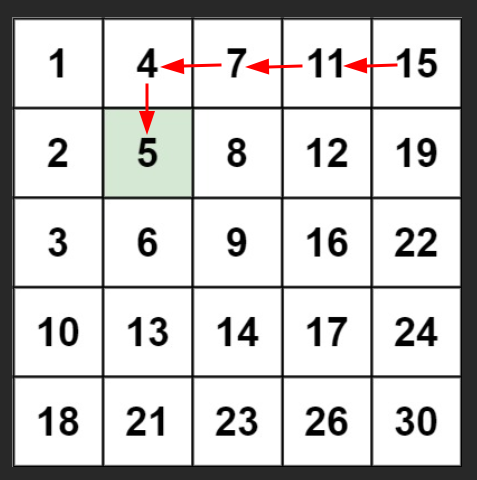
This worked fantastically (I struggled to get it right), drastically reducing the runtime.
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = 0, n = matrix[0].size()-1;
while(m<matrix.size() && n>=0){
if(matrix[m][n]==target) return true;
else if(matrix[m][n]>target) n--;
else m++;
}
return false;
}
};
The results
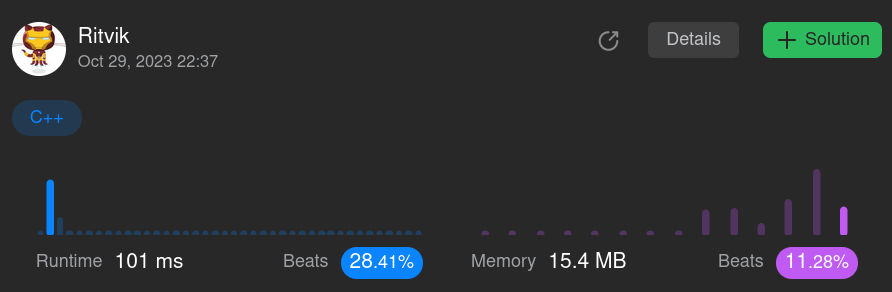From ~2700ms to ~100ms. The algorithm just got 27 times faster !
Minor Tinkering
I added a few performance-boosting tricks, such as turning off synchronization with C's standard streams and clearing the matrix after finding the solution.
It was just adding two lines of code std::ios::sync_with_stdio(false); and matrix.clear() and the final code was :
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
std::ios::sync_with_stdio(false);
int m = 0, n = matrix[0].size()-1;
while(m<matrix.size() && n>=0){
if(matrix[m][n]==target) {
matrix.clear();
return true;
}
else if(matrix[m][n]>target) n--;
else m++;
}
matrix.clear();
return false;
}
};
Aaaanddd here's a better result
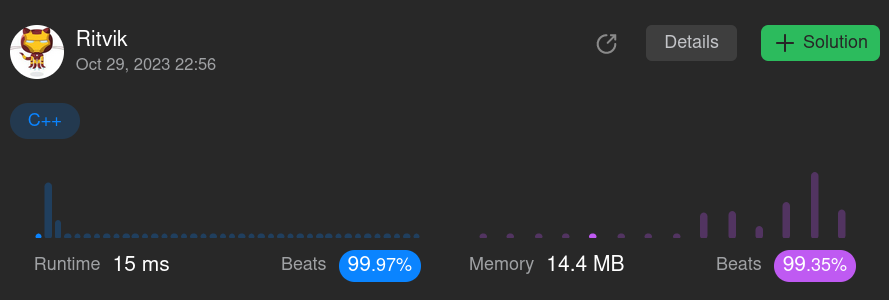Who knew 2 lines of code can bring down the time from 100ms to 15ms
I did (*chuckles) 😈
The Best Solution
Why settle for 99.97% beats where you're so close to a perfect 100 ?
I added a initial stopping condition (for empty matrices), converted int to short at necessary places and was thinking what else to do.
And suddenly, I realized something...the matrix given was sorted.
Yes, Binary search. I felt like a fool for not thinking about it the first time...but we're humans and humans make mistakes :)
Finally I wrote the perfect code
class Solution {
public:
inline bool searchMatrix(vector<vector<int>>& matrix, int target) {
std::ios::sync_with_stdio(false);
if (matrix.empty() || matrix[0].empty()) return false;
short m = matrix.size(),n = matrix[0].size();
if (target < matrix[0][0] || target > matrix[m-1][n-1]) return false;
for (short i = 0; i < m; ++i) {
if (matrix[i][0] <= target && matrix[i][n-1] >= target) {
short start = 0, end = n - 1;
while (start <= end) {
short mid = start + (end - start) / 2;
if (matrix[i][mid] == target) {
matrix.clear();
return true;
} else if (matrix[i][mid] < target) {
start = mid + 1;
} else {
end = mid - 1;
}
}
}
}
matrix.clear();
return false;
}
};
This approach intelligently exploits the sorted nature of the matrix. For each row, if the target lies within the range of the row, a binary search is executed.
The results were satisfying
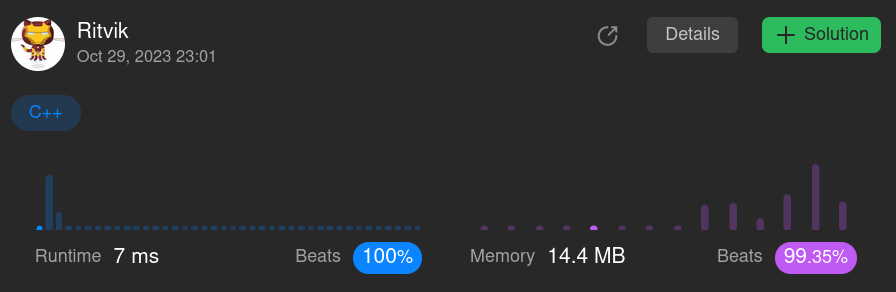
Yes, a perfect 100% in time beats and a near 100 ie. 99.35% in space beats.
When we look at the time taken by this optimized approach which is 7ms compared to the bruteforce approach which took 2700ms, we can see what we have achieved.
Conclusion
The journey of optimization is much like sculpting; you start with a raw piece and meticulously refine it, shaping it to perfection over time. Starting from a basic brute-force strategy and progressively refining, we achieved a solution that was a staggering 400 times faster than the initial attempt ! It's crucial to constantly seek patterns, delve into the intrinsic characteristics of the problem, and often, therein lies the roadmap to a more efficient solution.
Remember, perfection is seldom achieved in the first draft. It might elude us in the initial attempts, but with perseverance and a keen eye for detail, we inch closer to it with every revision.
Practice makes an algorithm perfect. Don't just solve, understand.
~ Ritvik